Probabilistic Models

Aim: compute probability distributions \(P\left(Q_{1} \ldots Q_{k} | e_{1} \ldots e_{k}\right)\)
\(Q_i\): query variables, on left side of probability distribution
\(e_i\): evidence variables, on right side of probability distribution
hidden variables, in the overall joint distribution, but not in the queried distribution
naive: specifies a probability for every possible world \(\rightarrow\) joint distribution of every possibility
exponential in \(n\) number of variables
Inference by Enumeration: Gather all rows consistent with evidence \(\rightarrow\) sum out hidden variables \(\rightarrow\) normalize
Independence: joint distribution = product of marginal distributions
\(P(x, y) = P(x) P(y)\) or \(P(x|y) = P(x)\)
linear instead of exponential
Independence is rare, conditional independence is more common
Conditional Independence:
\(P(X, Y | Z) = P(X|Z)P(Y|Z)\)

Example Bayes Net
Source: CS 188
Inspiration: storing all \(n\) joint distributions take \(O(d^n)\) space
Solution: describing joint distributions with simple, local distributions (conditional probabilities)
Nodes: variables with domains
Arcs: interactions encoding conditional dependence
Nodes are independent of its ancestors given its parents
shielding: when \(X \rightarrow Y \rightarrow Z\), \(Z\) is shielded from \(X\) by \(Y\)
- since knowing \(X\) won't give information on \(Z\) once \(Y\) is known
Calculate the probability of a given assignment with chain rule:
\(P\left(X_{1}, X_{2}, \ldots, X_{n}\right)=\prod_{i=1}^{n} P\left(X_{i} | p a r e n t s\left(X_{i}\right)\right)\)

Eliminate variables one-by-one
Eliminating \(X\): Join (multiply together) all factors involving \(X\), then sum out \(X\)
factor: unnormalized probability
each factor is proportional to the corresponding conditional probability
Example
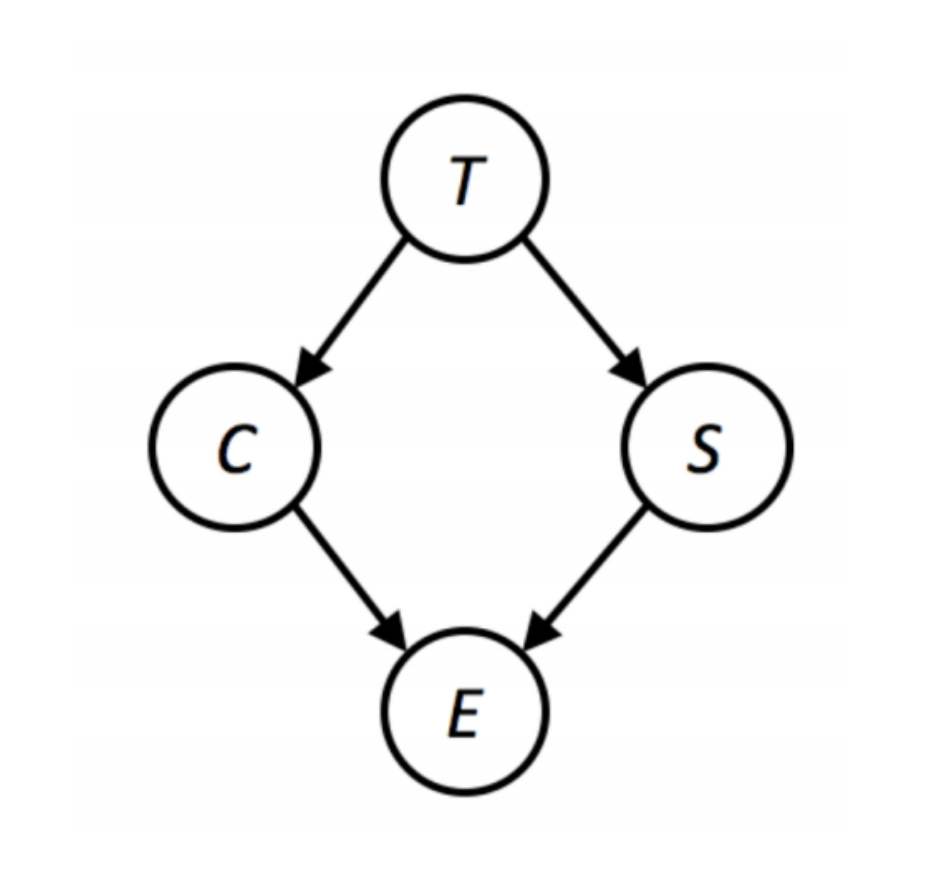
We have factors (probabilities) \(P(T), P(C | T), P(S | T), P(E | C, S)\)
Want to find: \(P(T|+e)\)
Procedure:
- Join all factors with \(C\), forming \(P(C,+e | T, S)=P(C | T) \cdot P(+e | C, S)\)
- Sum out \(C\), giving \(P(+e | T, S)\)
- Join on \(S\), giving \(P(+e, S | T) = P(+e | T, S) \cdot P(S | T)\)
- Sum out \(S\) to find \(P(+e | T)\)
- \(P(+e) = \sum\limits_T P(+e | T) \cdot P(T)\), \(P(T | +e) = \frac{P(+e | T) P(T)}{P(+e)}\)

Inspiration: direct inference is slow (NP-hard)
Solution: simply count samples
Naive: prior sampling, simply using the conditional probabilities
Rejection sampling: reject any samples inconsistent with evidence
Likelihood weighting: set evidence variables to true and assigns a weight to the sample equal to the conditional probabilities
e.g.: for the example network, we want to sample \(P(T |+c,+e)\)
Start with \(w=1\)
For \(T\), since it's not an evidence variable, sample \(t_j\) from \(P(T)\)
For \(C\), since it's an evidence variable, set \(C\) to true and multiply \(w\) by \(P\left(+c | t_{j}\right)\)
For \(S\), since not evidence, sample from \(P(S | t_j\)
For \(E\), since evidence, set \(E\) to true and multiply \(w\) by \(P\left(+e |+c, s_{j}\right)\)
Gibbs sampling: randomize variable assignments, repeatedly pick one variable at a time and re-sample its assignment

collider: node at which arrows collide head to head
unblocked path: path (disregarding directions) without colliders or conditioned nodes
if a collider or one of its descendants are conditioned, it no longer blocks paths
\(x\) and \(y\) are d-separated if there is no unblocked path between them
if \(x\) and \(y\) are d-separated, they are conditionally independent given the conditions
if \(x\) and \(y\) are d-connected, they are not guaranteed to be conditionally independent
Source